Apuntes 1: Estructuras Metálicas - Miembros a Flexión

MIEMBROS A FLEXIÓN

Lo anterior es cierto solamente si la longitud "L" de la viga es menor a el valor "Lp" denominada longitud máxima no soportada lateralmente para la cual ocurre la plastificación de la sección, lo cual permite su rotación. A este comportamiento se le denomina pandeo plástico(L < Lp).

Si la longitud "L" de la viga es mayor que "Lp" pero menor que cierto valor "Lr" denominada longitud máxima no soportada lateralmente para la cual aún se presenta el pandeo lateral de la sección alcanzando el valor de fluencia en algunos de los puntos de la sección pero no en todos. A este comportamiento se le denomina pandeo inelástico(Lp < L < Lr).

Si la longitud "L" de la viga es mayor que "Lr", la viga se pandeara lateralmente "arrugándose" el patín a compresión, y si su rigidez torsional es baja se producirá falla por flexotorsión. En este caso no se alcanza el valor de Fy en ningún punto debido a flexión, llamado pandeo elástico ( L > Lr).
 
 

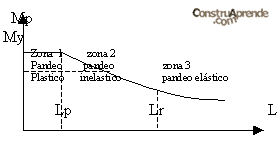
Los valores de Lp y Lr dependen de la sección transversal del miembro, del esfuerzo de fluencia del material empleado, así como de los esfuerzos residuales presentes en el miembro de tal forma que los valores de Lp y Lr están tabulados para cada sección en el AISC, mientras que en las NTC-Metálicas del RCDF – 87, se dan expresiones para calcularlas.
 

COEFICIENTES DE FLEXIÓN:

En los casos en que el tramo no soportado lateralmente (tramo de diseño) se encuentra flexionado en curvatura doble, o bien en curvatura simple, pero los momentos en los extremos de dicho tramo son mayores que el de cualquier punto intermedio, se aplican coeficientes de flexión "c" para ajustar (amplificar) los valores resultantes del caso base (curvatura simple con momentos extremos menores que en cualquier punto intermedio) para obtener los momentos nominales que verdaderamente alcanzará la sección estudiada bajo el diagrama de flexión en tensión.

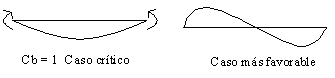
La razón de la amplificación de los valores de Mn* (base), se debe a que el caso base es el más crítico, mientras que cuando el tramo se flexiona en curvatura doble tenemos mayor restricción al pandeo.

Cb>1

Cb = 1 Caso crítico Caso más favorable

De acuerdo a las NTC- Metálicas

para curvatura simple

para curvatura doble

C = 1 cuando el momento en cualquier sección dentro del tramo no soportado lateralmente es menor que M₂y cuando el patín no esta soportado lateralmente de forma efectiva (en alguno de los extremos).

M₁ = momento menor de diseño en el tramo L (del extremo).
M₂= momento mayor de diseño en el tramo L (del extremo).

DISEÑO DE MIEMBROS A FLEXIÓN

En el diseño de miembros a flexión deberán considerarse los estados límite de falla siguientes:

• Formación de mecanismos con articulaciones plásticas.
• Agotamiento de la resistencia a flexión en miembros que no admiten redistribución de momentos.
• Iniciación del flujo plástico en la sección crítica.
• Pandeo local del patín comprimido (S4).
• Pandeo local del alma por flexión (S4).
• Plastificación del alma por cortante.
• Pandeo local del alma.
• Pandeo lateral por flexotorsión.
• Flexión y fuerza cortante combinados.
• Otras formas de pandeo del alma.
• Fatiga.

Además deberán considerarse los estados límite de servicio por deformaciones y vibraciones excesivas. 

RESISTENCIA DE DISEÑO EN FLEXIÓN

La resistencia de diseño en flexión Mr de una viga o trabe de eje recto y sección transversal constante se determina como se indica a continuación:

Miembros soportados lateralmente (L £ Lu)

Lu = Longitud no soportada lateralmente para la que el miembro puede desarrollar todavía el momento plástico Mp, no se exige capacidad de rotación.

Para este caso en que el patín se encuentra soportado lateralmente de forma continua, o bien la distancia entre soportes laterales L < Lu es igual a:

• Para secciones 1 o 2:

Mr = FrZFy = FrMp
Fr = 0.9

Para secciones IE, IR, IS: 

Para secciones OR: 

Donde:

Mp = Momento plástico resistente de la sección .
M₁ = Menor de los momentos extremos en el tramo no soportado lateralmente.
ry = radio de giro de la sección con respecto del menor momento de inercia de la sección.
M₁/Mp > 0 si el tramo se flexiona en curvatura doble.
M₁/Mp < 0 si el tramo se flexiona en curvatura simple.

El patín comprimido debe soportarse lateralmente en todas sus secciones en que aparezcan articulaciones plásticas.
 

 
• Secciones tipo 3:

Mr = FrSFy = FrMy

Donde:

S = Módulo elástico de la sección
Fr = 0.9
My = Momento elástico de la sección (inicio de fluencia)

Para secciones IR, IS, IE, flexionada en torno a cualquier eje centroidal principal puede tomarse un valor de Mr comprendido entre FrMy calculado por interpolación lineal de acúerdo a los valores correspondientes a 830/Ö Fy y 540/Ö Fy de las relaciones ancho espesor de patines:

FrMp Þ 830/Ö Fy
FrMy Þ 540/Ö Fy

Si la flexión es en torno al eje de mayor momento de inercia se comprobará que la relación ancho / espesor del alma no excede de la correspondiente al valor calculado de Mr para la cual también se interpolará linealmente entre las relaciones: 8000/Ö fy y 5000/Ö fy correspondientes a FrMpy FrMy respectivamente.

No hay límites en la longitud L (no apoyada lateralmente) en seccione 1, 2, 3 o ensecciones OR, OS, OC o bien cuando la viga sea cual fuere su sección transversal, se flexiona alrededor de su eje de menor momento de inercia. Por lo tanto, en estos casos Mr se determina como:

Mr = FrMp ó Mr = FrMy
 
 

• Secciones tipo 4:

Cuando el alma como el patín comprimido son tipo 4 Mr se determina con los criterios de diseño de perfiles de pared delgada dobladas en frío.

Cuando las almas son tipo 1, 2 o3 y los patines tipo 4 se tendrán dos casos:
 
 

c.1) Si el patín comprimido esta formado por elementos planos no atiesados:

Mr = FrQsSFy = FrQsMy

c.2) Si el patín esta formado por elementos planos atiesados:

Mr = FrSeFy

Donde:

Se =Módulo de sección efectivo del elemento obtenido con el ancho efectivo "be" del elemento.

Miembros no soportados lateralmente L > Lu

La resistencia de diseño a flexión cuyo patín comprimido esta provisto de soportes laterales con separaciones mayores que Lu es:

1. Para secciones 1 o 2 con dos ejes de simetría , flexionados alrededor del eje de mayor momento de inercia:

Si 

Si 

Mp = Momento plástico
Mu = Momento resistente nominal de la sección por pandeo elástico
Lr = Longitud que separa los intervalos de aplicación de las 2 ecuaciones anteriores

Mu = es ¹ al de diseño

Para vigas con secciones IE, IR, IS, laminadas o hechas con tres placas soldadas, el momento resistente nominal de la sección Mu cuando el pandeo lateral es en la zona elástica se determina como:

En secciones IE, IR, IS, laminadas o hechas con placas de dimensiones semejantes a las laminadas puede tomarse:

donde:

En las ecuaciones anteriores:

Fr = 0.9
A = área total de la sección
d = peralte
Iy = momento de inercia mínimo de la sección
Ry = radio de giro
t = espedor del patín comprimido
L = longitud de la viga no soportada lateralmente del patín
J = Constante de torsión de Sant – Venant
Ca = alabeo por torsión
C = coeficiente de flexión
C = 0.6 + 0.40 M₁/M₂ para curvatura simple
C = 0.6 - 0.40 M₁/M_{2 ³}0.40 para curvatura doble
C = 1 cuando el momento flexionante en cualquier sección dentro del tramo no soportado lateralmente es mayor que M₂. Cuando el patín no esta soportado lateralmente efectivamente en uno de los extremos.
M₁ = menor momento en el tramo de diseño L
M₂ = mayor momento en el tramo de diseño L
Para secciones rectangular hueca (OR) Ca = 0

EXPRESIONES PARA CALCULAR LOS VALORES DE Lu Y Lr EN MIEMBROS DE SECCIONES IE, IR, IS.

• Para secciones S₁ o S₂ con dos ejes de simetría a flexión en torno a x . Miembros de sección IE, IR, IS:

Para estas mismas secciones o las hechas con placas soldadas de dimensiones semejantes a las laminadas se podrán emplear las expresiones simplificadas:

donde:

siendo:

t = espesor el patín a compresión
d = peralte total de la sección

Expresiones para el cálculo de Lu, Lr en secciones OR, OS, OC en S1 Y S2.

Ca = 0 Mu = es la misma expresión anterior

 
 
• Secciones S₃, S₄ con dos ejes de simetría y canales en los que esta impedida la rotación en torno al eje longitudinal ( restringida a torsión ). Flexionadas alrededor de su eje principal mayor.

Si 

Si 

Donde:

Mu = momento resistente nominal en pandeo elástico obtenido por cualquiera de las ecuaciones dadas anteriormente:

• Para canales Mc₂ = 0
• Para OC Ca = 0

Lu, Lr se determinan con las expresiones dadas anteriormente pero al determinar Xu, Xr, Lu y Lr se cambiará Zx por Sx.

• Para determinar el Mu (el momento resistente nominal) en pandeo elástico para vigas formadas por miembros tipos canal (CE), se emplea la fórmula:

Mu = 1/c Mc₁

Siendo:

b.2) Para secciones S4 donde el alma es S4, patín S1, S2 y S3:

donde:

Aa = Área del alma
Ap = área del patín comprimido
h = peralte del alma
t = grueso del alma
S = módulo de sección elástico respecto del patín comprimido (Ixp/C)